Joule-Kelvin Effect | Medical Physics

A Mathematical Treatment of the Joule-Kelvin Effect

Consider a volume of gas at a high pressure and has internal energy, . The gas must do work on the gas already in the lower pressure region, and the gas may change its temperature such that the internal energy in the lower pressure region is .

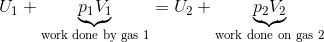
Enthalpy

Enthalpy is defined as

H=U+pV,

where U, p, and V are respectively the internal energy, pressure, and volume.

dH=TdS+Vdp

We can see that this process conserves enthalpy.

We want to know how the temperature changes at constant enthalpy when we reduce the pressure, demonstrated by the following relationship:

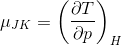
Using the reciprocity theorem and the definition of heat capacity, we obtain the following:

Maths Prerequisites:

Partial Differential - Reciprocity Theorem and Clairaut's Thoerem

(1)

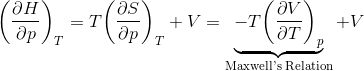
(2)

By substituting equation (2) into equation (1):

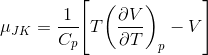
The inversion temperature occurs when

Heat Capacity at constant pressure,

Heat capacity measures temperature change when a given heat is supplied to a system.

At constant pressure, this is

For helium, the inversion temperature is 43K.

Maxwell's Relations

Because thermodynamic potentials (internal energy, enthalpy) are exact differentials,

using Gibbs energy,

dG=-SdT+VdT

we obtain:

References:

Blundell S J and Blundell K M, "Concepts in Thermal Physics: Second Edition", Oxford University Press, Oxford (2010)