Physics of Medical Scans
Biot-Savart Law
The Biot-Savart Law is a mathematical description of the magnetic field generated by a constant electric current.
An MRI scanner requires a static and uniform magnetic field.
In this section, we look at how different combinations of coils can be used to generate a uniform magnetic field.

The magnetic field of a coil with radius a is therefore:

Fig.1: The diagram shows the set-up used in the calculation of the magnetic field of a coil using Biot-Savart Law.

For a magnet displaced at x=-b, the magnetic field becomes

We can Taylor expand this equation for both two coils carrying the same current, and two coils carrying opposite currents:
Maths Prerequisites:
-
Integration
-
Vector Product
-
Taylor Expansion
Derivation:
Magnetic Field for a Current-Carrying Loop
Due to symmetry, the y-component is zero.
[4]


Helmholtz Coils
Taylor Expansion

The two coils carry the same current and are separated by a distance b=1/2 a. This cancels the x-squared term:

Maxwell Coils
Maxwell coils generate an even more uniform magnetic field than Helmholtz coils.
Two coils with radius a are placed a distance away from each other, and carry current I, and a coil with radius is placed at the mid-point, carrying current .
This cancels out the fourth order term. [3]
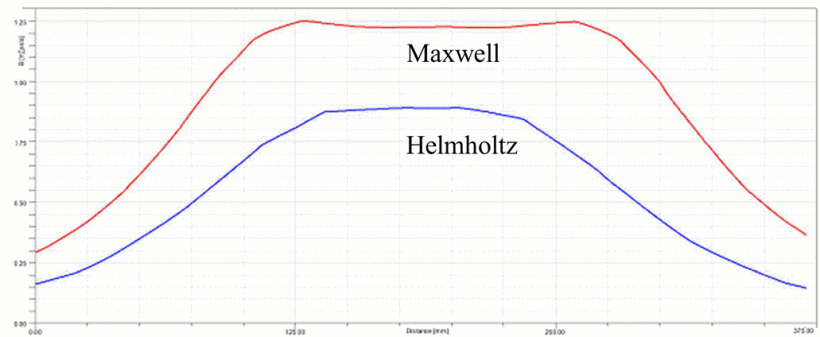
Fig.2: The plot shows how the magnetic flux density varies with distance for the Maxwell Coils (Red) and the Helmholtz Coils (Blue), where the x-axis is the distance from the centre of the first coil, and the y-axis is the magnetic flux density.
The approximately horizontal region represents the region where the magnetic field is approximately uniform.
As we can see, Maxwell coils provide a greater range, within which the magnetic field is roughly uniform.
Source: Mihailescu B, Plotog I, Velcea M, "Comparative Assessment of Maxwell and Helmholz Coils Magnetic Field for Biotechnological Application

Fig.3: The diagram shows an example of Maxwell Coils, where the two coils on the side have a smaller radius than the coil in the middle.
Source: Maxwell J. C, "A Treatise on Electricity and Magnetism Volume 2", Oxford University Press, Oxford (1891)
References:
[1] Ansorge R and Graves M, "The Physics and Mathematics of MRI", Morgan and Claypool Publishers, Bristol, (2016)
[2] Maxwell J.C, "A Treatise on Electricity and Magnetism Volume 2", Oxford University Press, Oxford (1891)
[3] Ansorge R and Graves M, "The Physics and Mathematics of MRI", Morgan and Claypool Publishers, Bristol, (2016)
[4] Young H. D and Freedman R. A, "University Physics Plus Modern Physics: 13th Edition", vol 2, Pearson Education, London (2012)